Binární sčítačka (na stavebnici Saimon)

Autorem článku je Ing. Lukáš Krejčík

Co to taková sčítačka binárních čísel vlastně je?

Než odpovím, zkusím popsat situaci, kdy já, člověk, chci sečíst dvě čísla. Pro začátek zvolím jednoduchá čísla, třeba 1 + 1. To umím – výsledek je 2. To je snadné. Kdybych byl ale počítač, byla by situace trochu jiná… Nebo nebyla?

Pojďme se na situaci podívat

Začneme také s jednoduchým součtem. Nejmenší jednotka informace, se kterou počítač umí pracovat, je 1 bit (z anglického Binary digit). Situace, kterou budeme řešit, bude sestavení obvodu, který sečte dva bity. Bity nabývají hodnoty 0 nebo 1. Někdy se setkáme s výrazy logická 0, nebo logická 1. Z hlediska elektrického obvodu pro nás logická 0 znamená stav, kdy v části obvodu nenaměříme napětí (například ledka nesvítí). Naproti tomu logická 1 pro nás bude znamenat stav, kdy napětí naměříme (ledka svítí).

Jak takové stavy sečíst?

Vyjdeme ze znalostí, které máme, totiž sečíst jedničky a nuly tak, jak to známe ze školy. Například 1+1, 0+1 a tak dále. Všechny kombinace, které nám mohou nastat, jsem sepsal do následujících rovnic:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 2

Máme tu tedy rovnice, které mají vlevo dva vstupy a jeden výstup vpravo. Řešením by tedy mohl být obvod nějaké logické funkce. Jaké? Z prvních tří řádků by se mohlo zdát, že bychom mohli použít obvod logického součtu OR (například hradlo 7432). Avšak nastal nám problém v posledním řádku. V elektrickém obvodu neznáme žádný stav, který bychom nazvali „logická 2“ ( ledka buď svítí = logická 1, nebo nesvítí = logická 0).

Musíme na to jít jinak!

Binární zápis čísla 2 je „10“. Nečte se to „deset“ jak jsme zvyklí z desítkové soustavy, ale „jedna nula“. Já zapíšu kombinace znovu, tentokrát pomocí binárního zápisu. Všechny výsledky budu zapisovat dvojciferně:

0 + 0 = 00

0 + 1 = 01

1 + 0 = 01

1 + 1 = 10

Můžeme tedy použít obvod logické funkce?

Víme, že logické funkce mohou mít více vstupů, výstup mají ale vždy jen jeden. Jak si poradit? Je to jednoduché. Výsledky jsou dvojciferná čísla. Použijeme logické funkce dvě, pro každou cifru jednu. Aby bylo jasné, jak to myslím, přepíšu naše rovnice do tabulky.

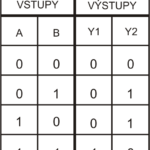
Sloupec Y1 bude výstup první logické funkce a sloupec Y2 bude výstup druhé logické funkce. Funkce Y2 reprezentuje součet vstupů. Funkce Y1 reprezentuje přenos do vyššího řádu. Ještě zbývá určit, o jaké logické funkce se bude jednat. Zkušené oko znalce pravdivostních tabulek uhodne, že ve sloupci Y1 jsou výsledky logické funkce AND. Ve sloupci Y2 se skrývá logická funkce XOR. Tedy Y1 = A AND B, Y2 = A XOR B. Zbývá jen navrhnout obvod, kterému budeme říkat poloviční sčítačka. Proč je poloviční, když obvod funguje přesně tak, jak chceme, vysvětlím později.

Pojďme sestavit obvod

Obvod můžeme sestavit na obyčejném nepájivém poli například pomocí hradel 7408 (4xAND) a 7486 (4x XOR). K tomu budeme potřebovat ještě pár spínačů a dvě ledky.

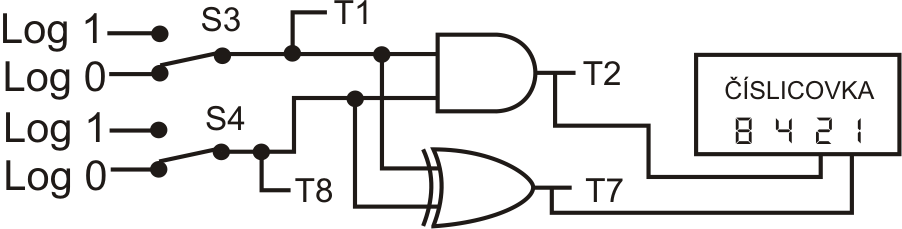
Já pro sestavení obvodu použil stavebnici Saimon, konkrétně základní modul Saimon 1 a rozšiřující modul Saimon 2 – logické funkce. Schéma zapojení na stavebnici uvádím na dalším obrázku.

Spínače S3 a S4 budou sloužit jako vstupy sčítačky. Testovací ledky T1 a T8 nám zobrazují stav vstupů. Svítí podle toho, zda vstup nabývá hodnoty logická 0, nebo logická 1. Výstupy hradel se zobrazují na testovacích led T2 a T7, kde uvidíme binární zápis výsledku. Rovněž jsou přivedeny na vstupy obvodu číslicovky s dekodérem, kde uvidíme sečtené číslo v desítkové (vlastně šestnáctkové) soustavě.

Na modulu Saimon 2 je nutné vyměnit integrovaný obvod 7432 za obvod 7486, abychom získali logickou funkci XOR. Z toho důvodu jsou integrované obvody umístěné v paticích. Na webových stránkách stavebnice je možné vytisknout si masku funkce XOR, aby nám seděly popisky.

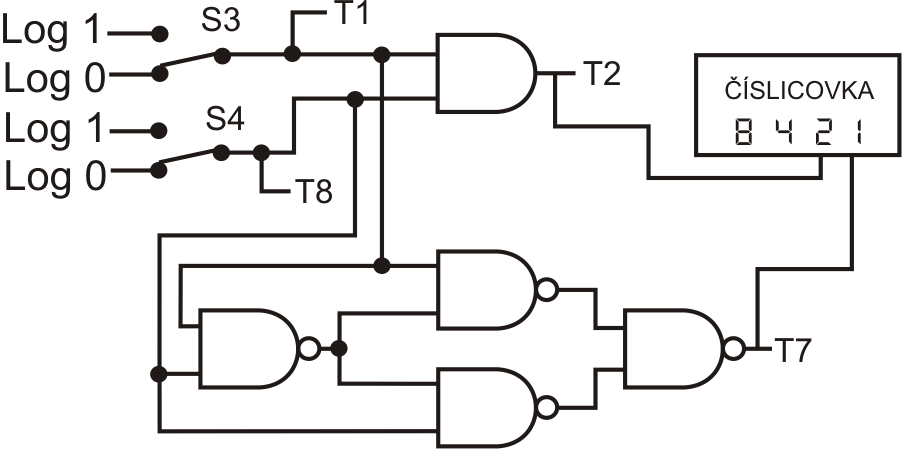
Pokud si na výměnu netroufáte nebo obvod 7486 nemáte, lze zapojit funkci XOR pomocí hradla NAND. Obvod pak vypadá následovně:

Celé zapojení na stavebnci Saimon je k dispozici na videu ZDE.

A jak je to s úplnou sčítačkou?

Když jsme sestavili poloviční sčítačku, určitě vás napadá, že musí existovat i úplná sčítačka. Jak se její funkce od poloviční sčítačky liší?

Poloviční sčítačka má dva vstupy (dva sčítané bity). Výstupy má také dva – součet a přenos do vyššího řádu. Pomocí takového obvodu můžeme sečíst dva bity. Náš cíl je ale sečíst čísla, například 4 + 6. Co s tím?

Vyjdeme z toho, že umíme sčítat bity. Takže kdybychom čísla zapsali v binárním tvaru, sečíst bychom je dokázali. Binární zápis 4 + 6 je 100 + 110. Napíšeme si čísla pod sebe:

100

110

Sčítat budeme tak, jako jsme se učili na základní škole. Sečteme každý řád pod sebou. První řád sečteme naší poloviční sčítačkou. Výsledek bude 0 + 0 = 0 s přenosem 0. Dále budeme sčítat druhý řád, tedy 0 + 1. Ale počkat! Je tu ještě přenos z předchozího sčítání! Ten musíme do rovnice započítat také. Musíme tedy sečíst 0 + 1 + 0. První dva vstupy jsou sčítané bity aktuálního řádu, tím třetím je přenos z předchozího sčítání. Obvod, který umí sečíst tyto tři vstupy, se nazývá úplná sčítačka.

Kolik sčítaček budu pro sčítání potřebovat?

Je patrné, že kolik mají sčítaná čísla řádů, tolik budeme potřebovat sčítaček. Každá sčítačka sečte bity stejného řádu. Na sečtení 4 + 6 tedy potřebujeme tři úplné sčítačky (i když na první řád nám stačí vlastně poloviční sčítačka).

Jak vypadá postup sčítání krok po kroku?

Sečteme 0 + 0 = 0, přenos 0. Dále sčítáme následovně – sečteme bity druhého řádu a přenos z předchozího 0 + 1 + 0 = 1, přenos do dalšího řádu je 0. Sečteme třetí řád a přenos z předchozího řádu 1 + 1 + 0 = 0 s přenosem 1. Přenos už nemáme s čím sečíst, napíšeme ho vlevo vedle výsledků sčítání. Celkový výsledek je 1010.

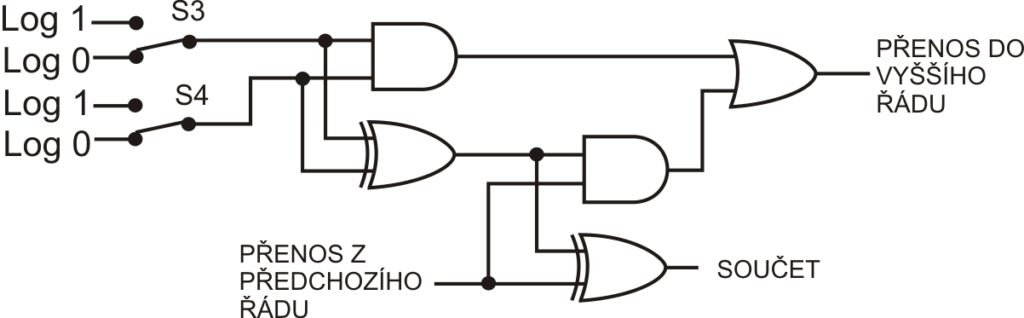
Zapojení úplné sčítačky

Obvod úplné sčítačky lze realizovat pomocí dvou polovičních sčítaček a funkce OR. Spínače S3 a S4 reprezentují sčítaný řád.

Závěrem

Přesto, že v dnešní době sčítání binárních čísel není na pořadu dne tak, jako dříve, tak věřím, že pochopení principů je stále stejně důležité. Já osobně miluju světélka, takže se mi na obvodu líbí monitorování vstupů pomocí testovacích led, indikace zapnutí integrovaných obvodů a zobrazení výsledku jak v binárním tvaru, tak v číselném.